An Attempt to Crack the Entombed Maze Generation Algorithm

Work in Progress

So I came across this problem in the List of unsolved problems in computer science - Wikipedia¹ on a boring Saturday evening when I was randomly browsing the web.

A bit of background

Entombed is an Atari 2600² game released in 1982. The game has a very simple gameplay. Try out the game here: Entombed

There’s a vertically scrolling maze (which is also symmetric) and player has to go through the maze avoiding enemies and picking up make-break boosters (which are useful for making a wall or breaking one)

The game has been subject to academic research particularly for its maze generation. Since the Atari 2600 had a limited ROM size, the mazes were too big to store on the ROM, and after researchers evaluated³ the game’s ROM, they found that the mazes were generated during runtime.

Defining the problem

The mazes that were produced in the game were unsolvable without efficient use of the make-break item (Which adds the game factor to it). However, during an interview with the Paul Allen Newell who previously worked on the game, it is said that they were able to come up with an algorithm which consistently generates solvable mazes in the interview with Paul Allen Newell⁴

The story of the algorithm is that one night after work, Duncan and I went out for a beer and ended up coming up with this “problem” of wondering whether one could generate an endless maze that always had a solution. At the time, we weren’t thinking of a game per se, it just seemed like an interesting puzzle for us to solve. We worked out the algorithm and, since I knew how to program a VCS system (Duncan was Vectrex only), I spent a weekend coding something up. We were surprised at the elegance of the algorithm as it gave us the ability to dial in a “difficulty factor” (via a bit setting) and we could prove that there was not only a point where it became unsolvable

(Here, “VCS” refers to Atari Video Computer System and not Version Control System)

So the question I was actually interested in is

Is it possible to come up with a maze generation algorithm which only produces a solvable maze using the 5 context bits (two bits to the left and three bits above)?

Simply upon inspection, we can see that the maze that is generated within the game itself is unsolvable. Although the title of this post is about Entombe and it’s mazes, we’re past that and I am starting to question why this problem is even on the list of unsolvable problems¹. The maze generated isn’t solvable and not special except for the aesthetics of it. A reddit thread about this in /r/programming seems to agree with me⁵, which sadly I stumbled upon only after spending enough time on this.

However, I will move on to defining a new problem and possibly try to answer it.

Solvability

A vertically scrolling maze of MxN grid (M width and N height) can be defined as solvable if you can add two empty rows on the top and bottom of the maze respectively to make it Mx(N+2) and there exists a path from the top row to the bottom row. This is more or less an informal definition, but very

For example, The maze given below is solvable

There exists a path from the top to the bottom

But the one below is not. No path is present

It is trivial to come up with an algorithm for generating mazes that are always solvable. A straight line path from top row to bottom row is solvable by definition, however we’re not interested in that, so our definition of mazes needs to be more tricky.

Definition for an Interesting maze

As mentioned, a maze which is just “Solvable” isn’t of particular interest. It is very trivial to generate it and solve it. So I am going to add 2 more criteria for the generated maze. I came up with these criteria after a bit of reference on mazes⁶

1. The maze should be simply connected or perfect, i.e, it should have no loops and should have one and only one solution.

This means that the maze should both be solvable and not be very easily solvable (like a hallway of empty blocks).

2. The maze should have at least one dead-end

A dead-end can be defines as an empty cell in the maze which is not the start or end cell and has only one path out of it. A maze without any dead-end will be a very easy one to solve, but instead, we want the maze to be challenging enough.

Now, I am defining an Interesting Maze as a maze which satisfies both 1. and 2.

So our problem definition becomes

Is it possible to come up with a maze generation algorithm which produces a solvable perfect maze with at least one dead-end^ using the 5 context bits (two bits to the left and three bits above)?

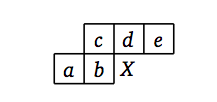X is generated using the bit values of a, b, c, d and e.

Attempting a solution

Before approaching the solution, my intuition for the answer is “No”, it is not possible to generate an Interesting maze with only using the given context-bits for generating the next bit.

Take P to be our initial Conjecture

P: It is possible to construct a vertically scrolling perfect maze with at least one dead-end using the cell values of previous two blocks in the same row and left, middle and right cells on the row above it

Assume our generated maze Z has a thick wall with two cells width on either sides (This doesn’t affect our original conjecture since adding solid walls on sides will not interfere with the original solution)

Ehhm… Waitt!!

As I was trying this out in paper to order to prove it, I actually was able to come up with a configuration that generates a perfect maze (with only one path and no loops) and with more than one dead-ends, although it doesn’t look very challenging, it does satisfy all the criteria and it is trivial to show that the maze will satisfy these conditions (Since no random selection is involved). Here is the configuration for those who are interested (You might want to toggle the first row to something like 1, 1, 0, 1, 1, 1, 1, 1, …)

Well, that was a bit disappointing

And even adding some randomness makes the maze a bit better, but still kinda not challenging.

Here, the ? indicates bits which are randomly chosen.

At least this one is a little bit better

Following are the rules used for this particular maze

		00110 - 1
		00111 - 0
		01000 - R
		01011 - 1
		01100 - 1
		01101 - 0
		10000 - 1
		10001 - 1
		10010 - 1
		10011 - 0
		11000 - 1
		11001 - 1
		11011 - 1
		11100 - 0
		11101 - 0

Okay, but this is not what I want, I want a maze that is challenging as well, and something that could be randomized although not strictly a requirement at the moment. So it’s time to re-define our “Interesting Maze” a little bit more so that it actually is interesting!

Work in Progress

References: